Rushil Roy asked this interesting question:
it is understood that light rays travel slower through denser medium (such as water/glass) compared to air. The same is true for sound waves, it has different speeds when it travels through different media. But why does light bend while sound doesn’t?
It is interesting that this question does not occur to most students (including me!) when they are studying in school.
Here is the answer, as far as I can tell:
Sound refracts just like light, but the issue is that we just don’t care as much.
Let’s go step-by-step through this.
We care far more about refraction of light and far less about refraction of sound because our eyes are able to very precisely locate the source of most light rays, whereas our ears are pretty bad at precisely locating the source of a sound. Where did a particular sound come from? The best we can do is “left” or “right” and “near” or “far”. So, even though sound refraction is happening all the time, we don’t really notice or care.
That brings us to the next question: why did our senses evolve in such a way that we can locate light precisely, but not sound?
The reason has to do with the fact that in case of sounds in day-to-day life, diffraction is a far more important phenomenon than refraction. Diffraction is the bending and spreading of waves when they encounter objects or slits of a size comparable to the wavelength of the wave. Now, the sound that humans are normally able to hear have wavelengths from 2cm to 2m (more precisely, 1.7cm to 1.7m; by contrast, visible light has wavelengths that are from 400 to 700 nanometers). And considering the number of different things in our environment that are of this size, sound waves are pretty much diffracting like crazy all over the place. Which makes it hopelessly confusing to precisely locate sources of sound.
This means that even if we had ears that were capable of precisely locating the source of a sound, it would be pointless because all the diffraction would completely confuse the system. In other words, precise location of sound is pretty much not worth trying for in most normal settings. (i.e. it wasn’t worth it for us to try to evolve precise sound-locating organs.)
There are two common situations where precise location based on sound waves becomes important. The first is echolocation used by bats. The other is ultrasonography (i.e. ultrasound imaging used in medical diagnostics). It is left as an exercise to the motivated reader to figure out why both these applications use “ultra” sound – i.e. 50KHz in case of bats, and 2 to 20 MHz in case of ultrasonography. (Hint: how is the frequency of the sound related to the wavelength?)
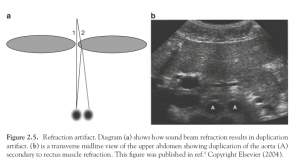
And refraction is an important effect in ultrasonography. Here is a picture, from a scholarly article on ultrasonography, talking about how, sometimes, multiple images of the same thing get created in an ultrasound image due to the effect of refraction.
Here is a colour picture of the same phenomenon, just because people like color:

Another interesting artifact of refraction of sound is the fact that sound appears to travel much farther at night or early morning.

Another mind-blowing aspect of refraction is this:
If light is going from point P in in one medium (e.g. air) to point Q which is in another medium (e.g. water), then the fastest path to go from point P to point Q (given the speed of light in the two media) is exactly the same path as that actually taken by light after refraction.
This is called Fermat’s Principle of least time. (And yes, this is the same Fermat, of the famous last theorem.)
Here is an interesting math problem which uses this principle. A lifeguard is sitting on a beach, some distance from the edge of the water. He becomes aware of a person drowning, as seen in the figure below. The guard must reach the swimmer in as little time as possible. Since the guard can run faster on sand than she can swim in water, it would make sense that the guard cover more distance in the sand than she does in the water. In other words, she will not run directly at the drowning swimmer. Your task involves determining the optimal entry point into the water in order to reach the drowning swimmer in the least amount of time.
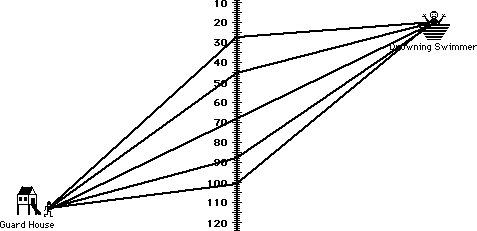
The solution to this problem is to use Snell’s Law of Refraction to determine the path of the lifeguard. The same principle also applies to shortest path via reflection. See Heron’s shortest path problem for an example. The advanced reader is encouraged to try solving the spider and the fly problem and spending some time wondering whether there is any relationship between that solution and Heron’s shortest path problem.
(Stuff like this makes me feel that I should should start a summer class for high-school students where we just discuss random science and maths stuff like this – no syllabus, no targets, no entrance-exam-coaching, just random discussions that start somewhere and end up somewhere else.)
